Linear Relationships

One of the most basic things a researcher is interested in is seeing whether there is any relationship between variables. Here, we will look at data from Nettle (1998).

Nettle recorded the number of languages, the area (in km2), the population, the mean growing season (MGS, in months), the number of weather stations measuring MGS, and the standard deviation of the measurements of MGS from the different weather stations in each country.

Plotting Correlations

We can use ggplot to see if there is any clear relationship between these variables. We might expect that there would be a relationship between the area of a country and the population of that country. We can use the geom_smooth and the geom_point functions to take a quick look.

rm(list = ls())

library(tidyverse)


df <- read.csv(url("https://raw.githubusercontent.com/ethanweed/ethanweed.github.io/master/r-tutorials/data/nettle_1998.csv"), sep = ";")


# Nettle reports the population data in 1000's, probably to save room in the data table, but that is an unusual number to think about population in, so let's convert to millions. While we're at it, let's convert km2 to millions, so that the number doesn't appear in scientific notation on the x-axis
df$Population <- df$Population*1000/1000000
df$Area <- df$Area/1000000

# For purposes of plotting, let's convert to a log scale
df$Population_log <- log(df$Population)
df$Area_log <- log(df$Area)
df$Languages_log <- log(df$Languages)

p1 <- ggplot(df, aes(Area_log, Languages_log)) + 
  geom_point() +
  geom_smooth(method = "lm") +
  theme_classic() +
  labs(y = "Number of languages (log)",
       x = (bquote('Area ((log) million km'^2*')')),
       title = "Number of Languages vs. Area")
p1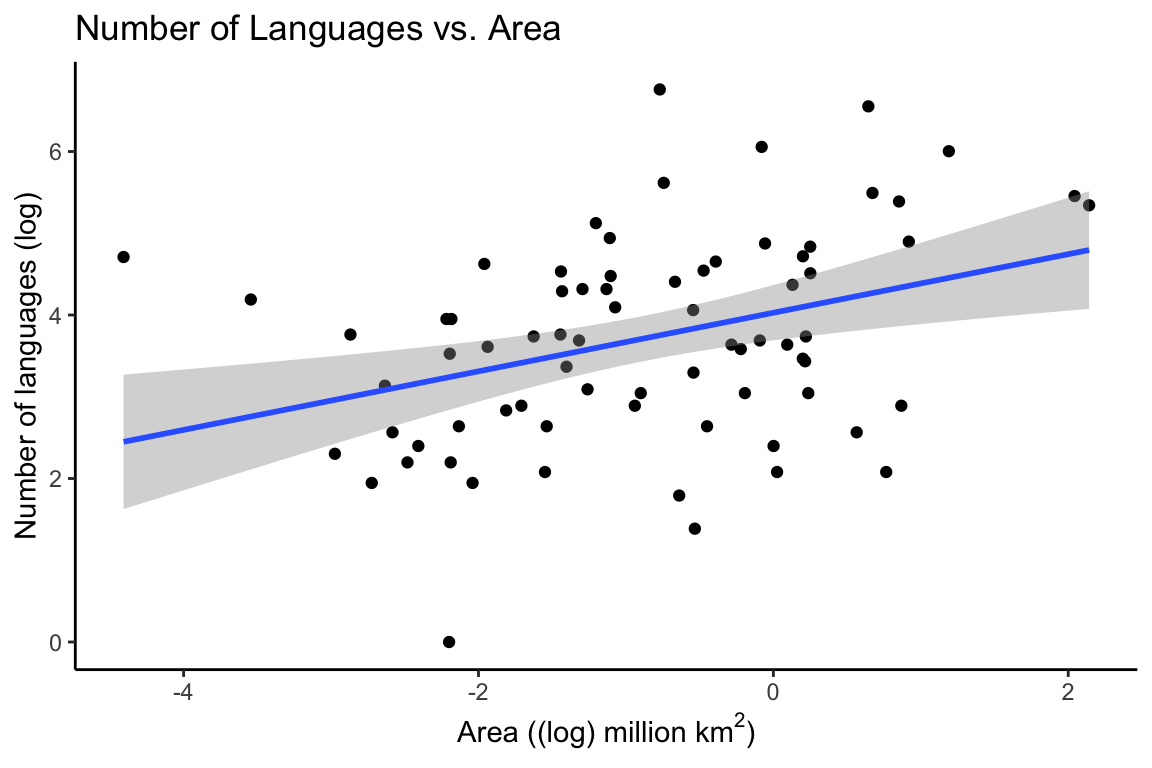

Modelling a Relationship as a Correlation

# load pander library to make a pretty output table
library(pander)

# if you don't want to bother with the pander library, you can just write "print(c)" or even just "(c)". Pander just makes the table output look nicer.

# do a correlation test to see how much the number of languages correlates with the area of the country
# and store the result in "c"
c <- cor.test(df$Languages, df$Area)

# alter the contents of c$data.name so that it doesn't say e.g. "df$Languages" in the output table
c$data.name <- "Languages and Area"

# output the results in a table
pander(c)
Pearson’s product-moment correlation: Languages and Area
Test statistic df P value Alternative hypothesis cor
2.576 72 0.01204 * two.sided 0.2905

The output tells us that there is a positive correlation between the number of languages and the area of the country. We can see this in the correlation coefficient (cor) which is 0.29. The correlation coefficient is a number between 1 and -1, with 1 indicating a perfect positive correlation, and -1 indicating a perfect negative correlation. The p-value of the correlation indicates how confident we can be in the fit of the model.

Correlation Matrix

Sometimes it can be useful to look at all the correlations between all of the variables in a dataset at once. This can be done with a correlation matrix. However, we should be careful about reading too much into a correlation matrix: it just tells us how much the variables correlate with each other. In order to be more rigorous about making predictions, we will need to build linear models.

df1 <- data.frame("Languages" = df$Languages, "Area" = df$Area, "Population" = df$Population, "MGS" = df$MGS)
df1$Languages <- as.numeric(df1$Languages)
pander(cor(df1))
  Languages Area Population MGS
Languages 1 0.2905 0.4088 0.2418
Area 0.2905 1 0.3331 -0.1277
Population 0.4088 0.3331 1 -0.01717
MGS 0.2418 -0.1277 -0.01717 1

Modelling a Relationship as a Linear Regression

In the plot above, we used a so-called linear model to draw the line between the points. The straight line in the plot is a linear model, that minimizes the distance between the line and every individual point. If we generate some random numbers to create white noise, then the line should be close to horizontal. Here we see a linear model of 1000 random numbers between 0 and 100 plotted against 1000 other random numbers between 0 and 100:

set.seed(42)

x = runif(1000, min=0, max=100)
y = runif(1000, min=0, max=100)

df_random <- data.frame("x" = x, "y" = y)

ggplot(data = df_random, aes(x,y)) +
  geom_point() +
  geom_smooth(method = "lm") +
  theme_classic() +
  labs(title = "White Noise")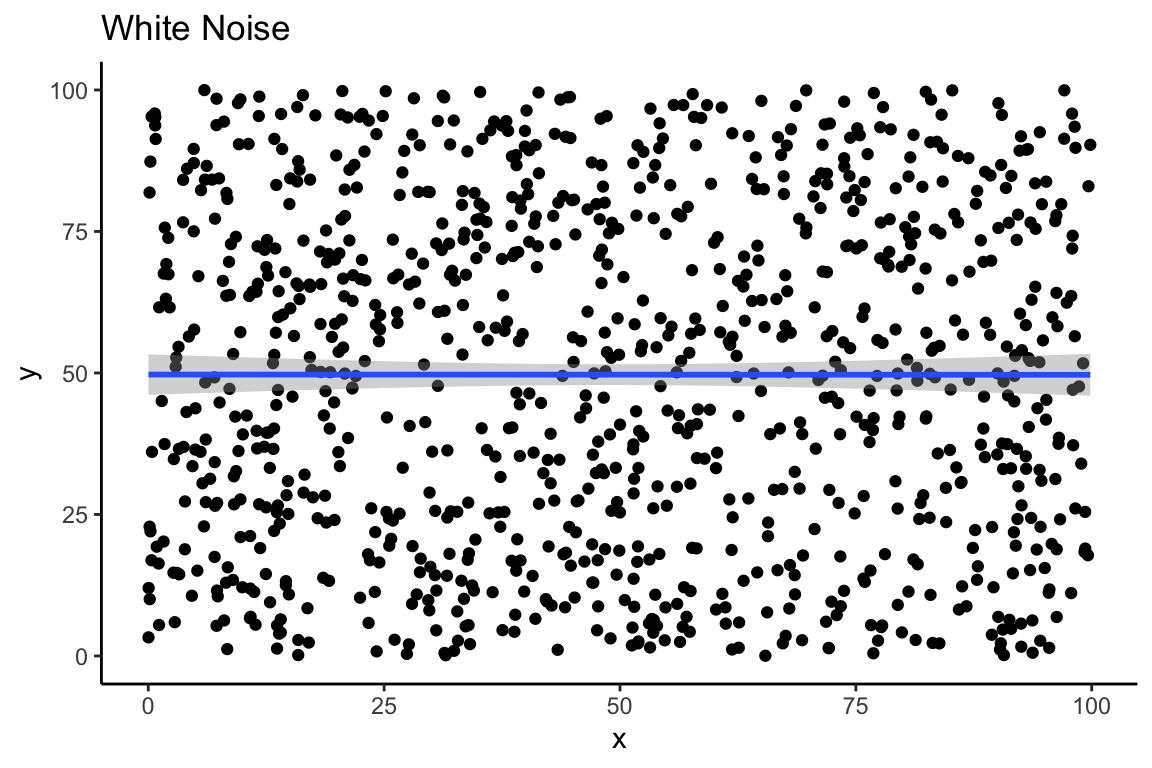

If we were in doubt, our correlation matrix shows us that there is very little correlation between these two vectors of random numbers:

pander((cor(df_random)))
  x y
x 1 -0.0004327
y -0.0004327 1

If we want to go beyond simply observing the correlation and instead use our linear model to make predictions about new data that we have not yet seen, we need to get the equation for our model’s line. That will allow us to extend the line in either direction, and make predictions.

The equation of a line is \(y=mx+y_0\), where \(y_0\) is the point at which the line intercepts the y-axis. This is sometimes also written as \(y=mx+b\), or \(y=ax+b\). These equations are all equivalant. The important thing for our purposes is that they define the slope and intercept of a line which represents a linear model of the data.

Linear models are very useful, and they are all over the place in statistics. In the case of our random, white-noise data, because the slope is nearly equal to zero, the intercept of the model is a very close approximation of the mean of y:

print(mean(y))
## [1] 49.70157
pander(summary(lm(data = df_random, y ~ x)))
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.72 1.829 27.19 2.86e-122
x -0.0004397 0.03217 -0.01367 0.9891
Fitting linear model: y ~ x
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
1000 29.63 1.872e-07 -0.001002 
mod <- lm(data = df, Languages ~ Area)

# if you don't want to use pander you can just write: summary(mod)
pander(summary(mod))
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.37 19.12 3.315 0.001437
Area 29.93 11.62 2.576 0.01204
Fitting linear model: Languages ~ Area
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
74 138.9 0.08439 0.07167

Modelling Multiple Predictor Variables in a Linear Regression

mod <- lm(data = df, Languages ~ Area + Population)
pander(summary(mod))
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 57.29 18.17 3.153 0.002366
Area 17.89 11.64 1.536 0.1289
Population 0.495 0.1594 3.105 0.002731
Fitting linear model: Languages ~ Area + Population
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
74 131.2 0.1939 0.1712 
# or you can just write: summary(mod)
library(ggpubr)

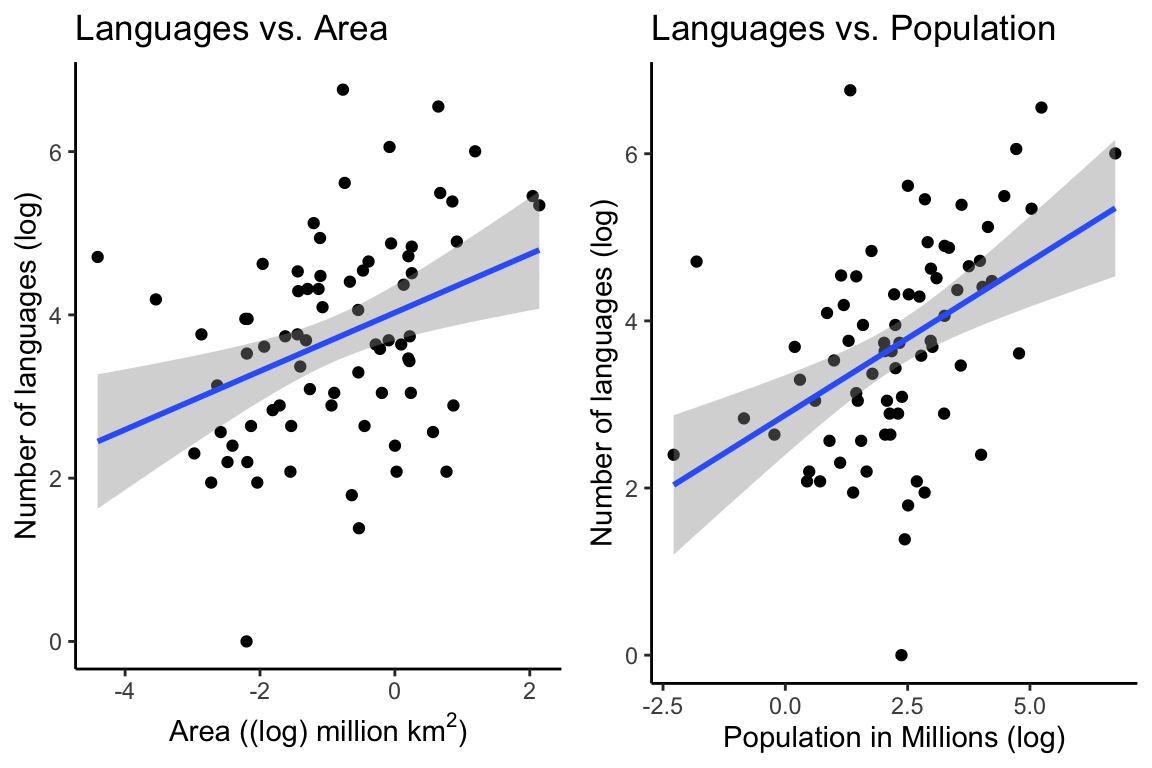
p1 <- ggplot(df, aes(Area_log, Languages_log)) + 
  geom_point() +
  geom_smooth(method = "lm") +
  theme_classic() +
  labs(y = "Number of languages (log)",
       x = (bquote('Area ((log) million km'^2*')')),
       title = "Languages vs. Area")


p2 <- ggplot(df, aes(Population_log, Languages_log)) + 
  geom_point() +
  geom_smooth(method = "lm") +
  theme_classic() +
  labs(y = "Number of languages (log)",
       x = "Population in Millions (log)",
       title = "Languages vs. Population")

ggarrange(p1, p2, ncol = 2)